PoyffffIfn n x and y B Partial derivative nfwrtX cxy is É x y s fx x y s his fathiffad if limit exists rate which f o's as we vary x holding y fixed Fix y define gox fax y then j Y't y If ix y s dy x iii To compute If regard y as constant differentiate w r t to x Y is defined and computed similarly Let f be a fan n x y and z Partials are defined similarly Second partial derivative 3 2,1 s How to use the difference quotient to find partial derivatives of a multivariable functions Example Using the definition, find the partial derivatives of f ( x, y) = 2 x 2 y f (x,y)=2x^2y f ( x, y) = 2 x 2 y For the partial derivative of z z z with respect to x x x, we'll substitute x h xh x h into the original function for x x x//googl/JQ8NysPartial Derivative of f(x, y) = xy/(x^2 y^2) with Quotient Rule
Www Ualberta Ca Rjia Math214 Part4 Lec2 Pdf
X/(x^2+y^2) partial derivative
X/(x^2+y^2) partial derivative-There are three partial derivatives f x, f y and f z The partial derivative is calculate d by holding y and z constant Likewise, for and 212 Partial Derivative as a Slope Example 26 Find the slope of the line that is parallel to the xzplane and tangent to the surface z x at the point x Py(1, 3, 2) Solution Given f x y x x y( , ) WANT In this case we call \(h'\left( b \right)\) the partial derivative of \(f\left( {x,y} \right)\) with respect to \(y\) at \(\left( {a,b} \right)\) and we denote it as follows, \{f_y}\left( {a,b} \right) = 6{a^2}{b^2}\ Note that these two partial derivatives are sometimes called the first order partial derivatives Just as with functions of one variable we can have derivatives of all orders



Www Ucl Ac Uk Ucahjva Multi4 Pdf
Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of the function and its derivatives Calculator supports derivatives up to 10th order as well as complex functions Derivatives are computed by parsing the function, applying differentiation rules andU_x = (y/z)*x^((y/z)1) u_y = lnx/z?Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi (Product) Notation Induction Logical Sets Pre Calculus Equations Inequalities Simultaneous Equations System of Inequalities Polynomials Rationales Coordinate Geometry Complex Numbers
By treating x as a constant, we find f y =3x 2 3y 2 Second Partial Derivatives Observe carefully that the expression f xy implies that the function f is differentiated first with respect to x and then with respect to y, which is a natural inference since f xy is really (f x) y For the same reasons, in the case of the expression, it is implied that we differentiate first with respect to yDerivative x^2(xy)^2 = x^2y^2 Natural Language;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge
If we consider a function like f (x,y) ˘x3y ¯x2y2, the partial derivatives are @f /@x ˘ 3x2y ¯2xy2 and @f /@y ˘ x3 ¯2x2y Each of these can of course be differentiated again, @2 f @x2 ˘6xy¯2y2, @2 f @y2 ˘2x2, @2 f @y@x ˘ @ @y µ @f @x ¶ 3x2 ¯4xy, @2 f @x@y ˘ @ @x µ @f @y ¶ ˘3x2y¯4xy We notice that the two mixed derivatives are equal In general the derivatives @2 f @x@y (aFind the indicated partial derivative(s) f(x, y, z) = e^{xyz^2} ;1 Topic 7 Self Assessment I Partial Differentiation 1 Find all first and second order partial derivatives of the following functions (i) y =x2 2xz z2 x z x




Partial Derivative Math Help Forum



Rules Of Calculus Multivariate
The partial derivative of a function of multiple variables is the instantaneous rate of change or slope of the function in one of the coordinate directions Computationally, partial differentiation works the same way as singlevariable differentiation with all other variables treated as constant The partial derivative of a function f (x, y) f(x,y) f (x, y) in the x x xdirection can beFor the function z = x2y3 Solution z = x2y3 ∴ ∂z ∂x = 2xy3, and ∂z ∂y = x23y2, = 3x2y2 For the first part y3 is treated as a constant and the derivative of x2 with respect to x is 2x For the second part x2 is treated as a constant and the derivative of y3 with respect to is 3 2 Exercise 1 Find ∂z ∂x and ∂z ∂y for each ofFor example, w = xsin(y 3z) Partial derivatives are computed similarly to the two variable case For example, @w=@x means difierentiate with respect to x holding both y and z constant and so, for this example, @w=@x = sin(y 3z) Note that a function of three variables does not have a graph 07 Second order partial derivatives Again, let z = f(x;y) be a function of x and y † @ 2z



Compute Partial Derivatives Of The Given Function Stumbling Robot




Partial Derivatives Worksheet
Please Subscribe here, thank you!!!So in the last couple videos I talked about partial derivatives of multivariable functions and here I want to talk about second partial derivatives so I'm going to write some kind of multivariable function let's say it's I don't know sine of X times y squared sine of X multiplied by Y squared and if you take the partial derivative you have two options given that there's two variables you canPartial Derivatives of f(x;y) @f @x "partial derivative of f with respect to x" Easy to calculate just take the derivative of f wrt x thinking of y as a constant @f @y "partial derivative of f with respect to y" Christopher Croke Calculus 115 Examples Compute @f @x and @f @y for f (x;y) = 2x2 4xy (xy3 xy)3 sin(xy y) x3y y x2 Christopher Croke Calculus 115 Examples Compute




Second Order Partial Derivatives Ucsd Second



17 5 Higher Order Partial Derivatives Graphing Calculator By Mathlab User Manual
The notation for partial derivatives ∂xf,∂yf were introduced by Carl Gustav Jacobi Josef Lagrange had used the term "partial differences" Partial derivatives fx and fy measure the rate of change of the function in the x or y directions For functions of more variables, the partial derivatives are defined in a similar way 1 For f(x,y) = x4 −6x2y2 y4, we have f x(x,y) = 4x3 −آلات حساب للجبر، حساب التفاضل والتكامل، هندسة، إحصاء، وكيمياء مع شرحThe cross partial derivative with respect to x and y is obtained by taking the partial derivative of f with respect to x, and then taking the partial derivative of the result with respect to y, to obtain / Schwarz's theorem states that if the second derivatives are continuous the expression for the cross partial derivative is unaffected by which variable the partial derivative is taken with




Multivariate Functions And Partial Derivatives Sage Research Methods




14 Partial Derivatives Copyright Cengage Learning All Rights
There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the other$ f_{xxx} $, $ f_{xyx} $ Answer $$24 x y^{2}6 y, 24 x^{2} y6 x$$ View Answer More Answers 0052 ag Alan G Topics Partial Derivatives Calculus Early Transcendentals Chapter 14 Partial Derivatives Section 3 Partial Derivatives Discussion You must be signed in to discuss Top Calculus 3 Educators AnnaAnswer to Let x^2 y^2 z^2 = 3xyz Find partial derivatives z_x, z_y By signing up, you'll get thousands of stepbystep solutions to your



Http Abel Math Harvard Edu Archive 21a Fall 09 Resources Chapter11 Supp Pdf




Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube
$$ ∂^2/∂x 8x^2y^4x^2 = 16y^42 = 2(8y^41) $$ Second Order Partial Derivatives The highorder derivative is very important for testing the concavity of the function and confirming whether the endpoint of the function is maximum or minimumPARTIAL DIFFERENTIATION 1 b) wx = −y2/x2, wy = 2y/x;Therefore at (1,2,4), we get wx = −4, w is more sensitive to changes in x around this point partial derivatives 2C Differentials;



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero




Partial Derivatives And Differentiability Sect 14 3 Flip Ebook Pages 1 Anyflip Anyflip
Exercise 1331 Use the definition of the partial derivative as a limit to calculate ∂ f / ∂ x and ∂ f / ∂ y for the function f(x, y) = 4x2 2xy − y2 3x − 2y 5 Hint Use Equations 1331 and 1332 from the definition of partial derivatives Answer ∂ f ∂ x = 8 x 2 y 3 ∂ f ∂ y = 2 x − 2 y − 2Let's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2xThe y derivative of f x(x, y) is ( f x) y = f xy = 6xy2 f xx and f xy are each an iterated partial derivative of second order The y derivative of the x derivative can also be written @ @y @ @x (x2y3) = @ @y (2xy3) = 6xy2 or @2 @y @x (x2y3) = 6xy2 Prof Tesler 31 Iterated Partial Derivatives Math C / Fall 18 2 / 19




Calculate The Second Order Partial Derivatives F X Chegg Com



Http Www Ams Sunysb Edu Jiao Teaching Ams261 Fall12 Lectures Larcalc9 Ch13 Pdf
Free partial derivative calculator partial differentiation solver stepbystep This website uses cookies to ensure you get the best experience By using this% \mathrm{נקה} \arcsin \sin \sqrt{\square} 7PARTIAL DERIVATIVE LINKSImplicit differentiation Partial derivative (i) y cos x = x^2y^2 (ii) e^z = xyz https//youtube/N6TLvbDCOUkLagrange's Multip
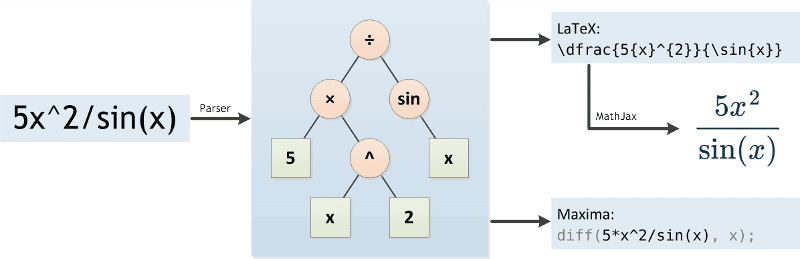



Derivative Calculator With Steps




2 Partial Differentiation
Approximations dx dy dz 2 3 2C1 a) dw = b) dw = 3x y2zdx 2x3yzdy x y2dz x y z c) dz = 2ydx−2xdy d) dw = tdu −udt (x y)2 t √ t2 −u2 2C2 The volume is V = xyz; Find the first partial derivatives of 1 f(x,y) = x^y 2 u = x^(y/z) Homework Equations The Attempt at a Solution f_x = y*x^(y1) f_y = lnx?To apply the implicit function theorem to find the partial derivative of y with respect to x 1 (for example), first take the total differential of F dF = F ydy F x 1 dx 1 F x 2 dx 2 =0 then set all the differentials except the ones in question equal to zero (ie set dx 2 =0)which leaves F ydy F x1 dx 1 =0 or F ydy = −F x 1 dx 1 dividing both sides by F y and dx 1 yields dy dx 1 = −
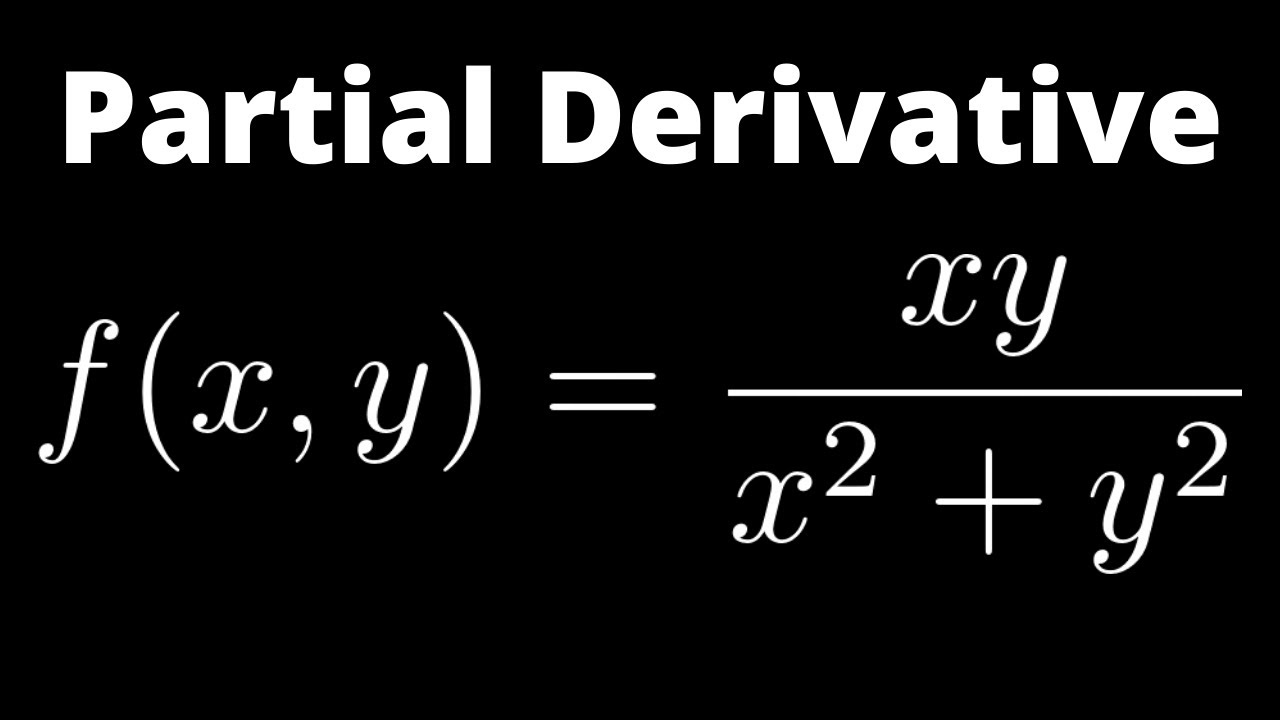



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube



Partial Derivatives Calculus Volume 3
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevelThis online calculator will calculate the partial derivative of the function, with steps shown You can specify any order of integration Enter a function Enter the order of integration Hint type x^2,y to calculate `(partial^3 f)/(partial x^2 partial y)`, or enter x,y^2,x to find `(partial^4 f)/(partial x partial y^2 partial x)` If the calculator did not compute something or you haveDerivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic & Comp Conic Sections Transformation Matrices & Vectors Matrices Vectors Geometry Plane Geometry Solid Geometry Conic Sections




Applications Of Partial Derivatives Use The Chain Rule To Find Dz Dt Z X 2 Y 2 Xy X Sin T Y 3e T Wegglab




Se13e01 01 Gif
Derivada parcial de x/ (x^2y^2) \square!So dV = yzdxxzdyI'm not really sure how to do these right =/ I would really appreciate any help Answers and Replies #2 jambaugh Science Advisor Insights Author Gold Member 2,307 297 Your f_x



Users Math Msu Edu Users Gnagy Teaching 10 Fall Mth234 W6 234 H Pdf




1 Given F X Y Z As Z 2 Y Find A The Partial Derivative F X Y Homeworklib
Answer f x = y sec 2 (xy) cos x and f y = x sec 2 (xy) Question 2 If f(x,y) = 2x 3y, where x = t and y = t 2 Derivative f with respect to t Solution We know, d f d t = ∂ f ∂ x d x d t ∂ f ∂ y d y d t \frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} \frac{\partial f}{\partial y}\frac{dy}{dt} d t d f = ∂ xPartial derivative of exp(x^2 y^2) Extended Keyboard;Partial derivative ofy/(x^2y^2) \frac{\partial}{\partial x} (2\times2) (2\times3) (3\times3) (3\times2) (4\times2) (4\times3) (4\times4) (3\times4) (2\times4) (5\times5) (1\times2) (1\times3) (1\times4) (1\times5) (1\times6) (2\times1) (3\times1) (4\times1) (5\times1) (6\times1) (7\times1) \mathrm{רדיאנים} \mathrm{Degrees} \square!



2




Partial Derivatives Calculus 3
(delw)/(delx) = x/sqrt(x^2 y^2 z^2) (delw)/(dely) = y/sqrt(x^2 y^2 z^2) (delw)/(delz) = z/sqrt(x^2 y^2 z^2) Since you're dealing with a multivariable function, you must treat x, y, and z as independent variables and calculate the partial derivative of w, your dependent variable, with respect to x, y, and z When you differentiate with respect to x, you treat y and zDefinition of Partial Derivatives Let f(x,y) be a function with two variables If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of f with respect to x which is denoted by Similarly If we keep x constant and differentiate f (assuming f is∂x∂y2, which is taking the derivative of f first with respect to y twice, and then differentiating with respect to x, etc In this manner we can find nthorder partial derivatives of a function Theorem ∂ 2f ∂x∂y and ∂ f ∂y∂x are called mixed partial derivatives They are equal when ∂ 2f ∂x∂y and ∂ f ∂y∂x are continuous Note In this course all the fuunctions we



Second Order Partial Derivatives In Calculus




Partial Derivative Examples Math Insight
Answer to Find the partial derivative of the function u=e^{x^2y^2z^2} By signing up, you'll get thousands of stepbystep solutions to your 1 This question already has an answer here Show that both mixed partial derivatives exist at the origin but are not equal (1 answer) Closed 2 years ago I am asked to show, that is everywhere two times partial differentiable, but itFind the indicated partial derivative(s) $ f(x, y) = x^4y^2 x^3y $;




Find The First And Second Order Partial Derivatives Chegg Com



1
For a function of two variables z = f(x,y) the partial derivative of f with respect to x is denoted by ∂f ∂x and is obtained by differentiating f(x,y) with respect to x in the usual way but treating the yvariable as if it were a constant Alternative notations for ∂f ∂x are f x(x,y) or f x or ∂z ∂x Example 2 Find ∂f ∂x for (a) f(x,y) = x3 xy2 y, (b) f(x,y) = x2y xy3Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Where the three partial derivatives f x, f y, f z are the formal partial derivatives, ie, the derivatives calculated as if x, y, z were independent ∂w Example 2 Find , where w = x3y −z2t and xy = zt ∂y x,t Solution 1 Using the chain rule and the two equations in the problem, we have ∂w ∂z x = x 3 −2zt = x 3 −2zt = x 3 −2zx ∂y x,t ∂y x,t t Solution 2 We take the



Search Q Product Rule Tbm Isch




Partial Differentiation If Z X Y X 2 Y 2 Show That әz әx әz әy 2 4 1 әz әx әz әy Youtube
F_{xyz} 💬 👋 We're always here Join our Discord to connect with other students 24/7, any time, night or day and the partial derivative of f at ( a, b) with respect to y, denoted by ∂ f ∂ y ( a, b), is defined as (222) ∂ f ∂ x ( a, b) = lim h → 0 f ( a h, b) − f ( a, b) h Note The symbol ∂ is pronounced "del" Recall that the derivative of a function f ( x) can be interpreted as the rate of change of that function in the
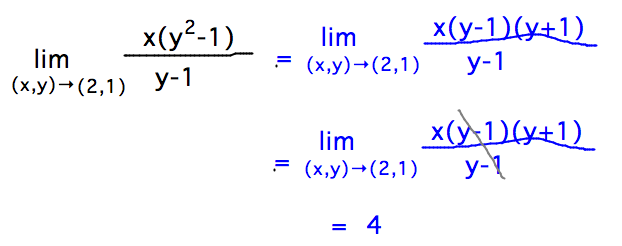



Geneseo Math 223 03 Partial Derivatives




Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange



People Math Harvard Edu Knill Teaching Summer13 Handouts Week3 Pdf



Partial Derivatives




Answered 2 Evaluate The Limit Using The Bartleby




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y




Using The Appropriate Properties Of Ordinary Derivatives Perform The Following A Find All The First Partial Derivatives Of The Following Functions F X Y I X 2 Y Ii X 2 Y 2 4 Iii Sin X Y Iv Tan




Second Order Partial Derivatives F X Y Sqrt X 2 Y 2 Youtube



Is X Iy X 2 Y 2 Analytic Function Quora




Derivative Calculator Wolfram Alpha




Step By Step Partial Derivative Solution Sample




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download




Answered 7 Find The Second Partial Derivatives Bartleby



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch15 Pdf



Partial Derivatives




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download
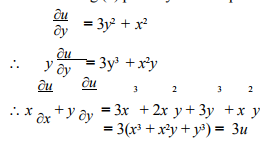



Partial Derivatives Differentiation Business Mathematics Statistics B Com Notes Edurev



Www Usna Edu Users Oceano Raylee Sm223 Ch14 3 Stewart 16 Pdf




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube




Second Partial Derivative Test Article Khan Academy




Partial Differentiation Application Ppt Download
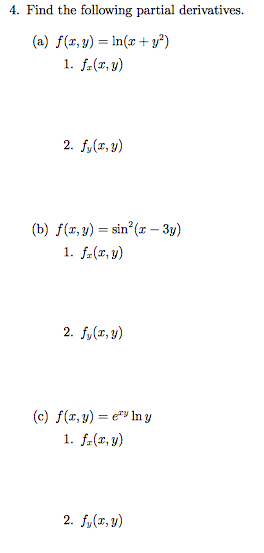



4 Find The Following Partial Derivatives A Chegg Com
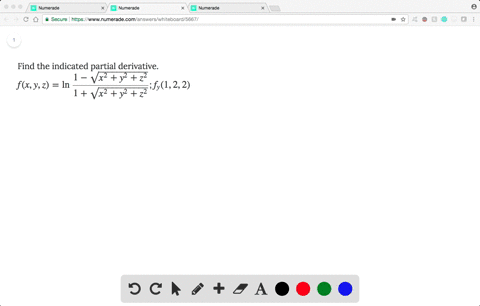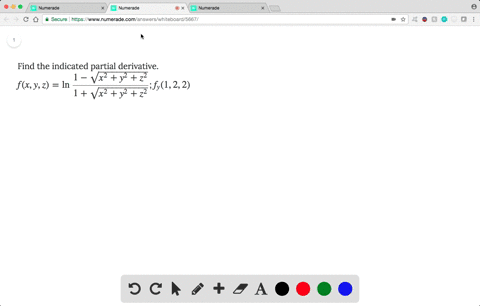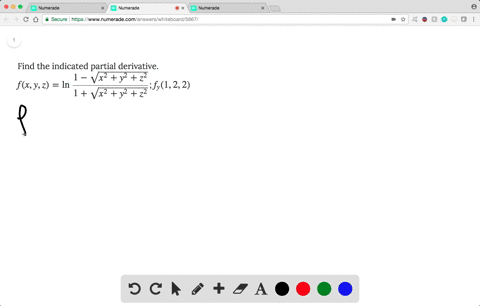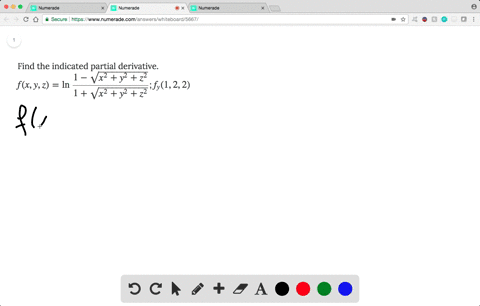



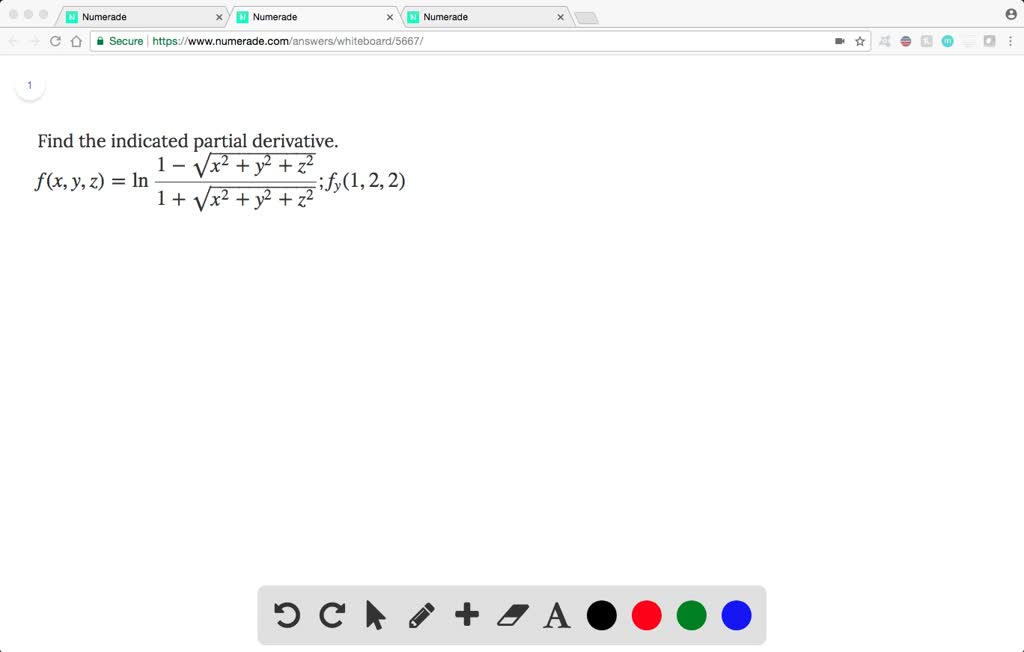
Solved Find The Indicated Partial Derivative F X Y Z Ln Dfrac 1 Sqrt X 2 Y 2 Z 2 1 Sqrt X 2 Y 2




Partial Differentiation And Multiple Integrals Pdf Free Download




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange




Partial Derivatives Archives Www Tinspireapps Com Blog
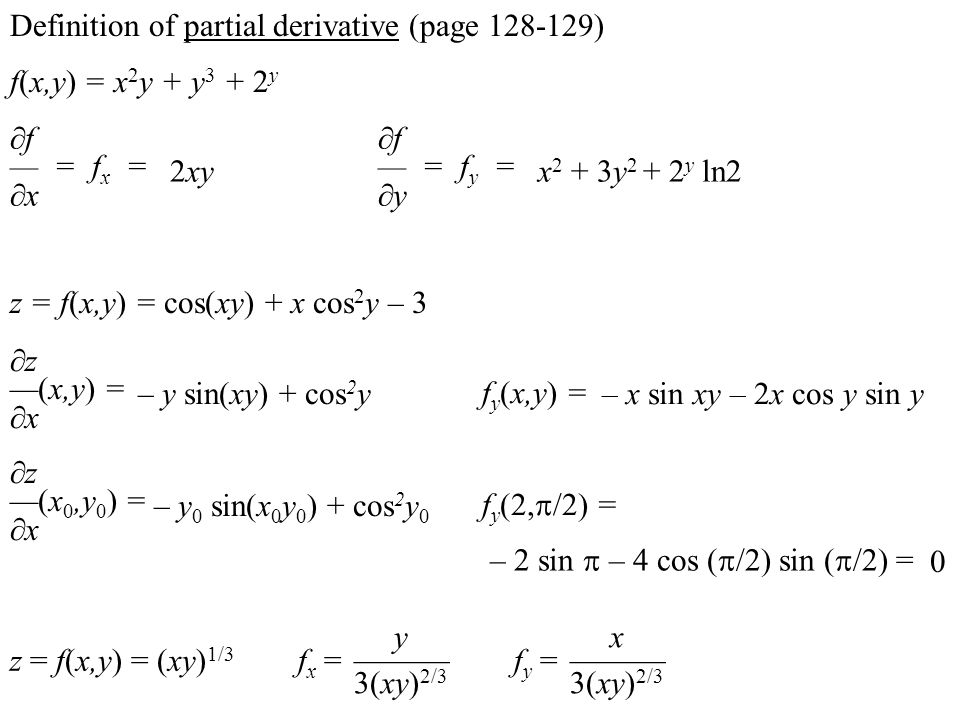



F X Y X 2 Y Y Y F F X X 2xyx 2 3y Y Ln2 Z F X Y Cos Xy X Cos 2



Www Ualberta Ca Rjia Math214 Hwks Sol8 Pdf




Find All The First Order Partial Derivatives For The Chegg Com



Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau




Partial Differentiation And Multiple Integrals Pdf Free Download
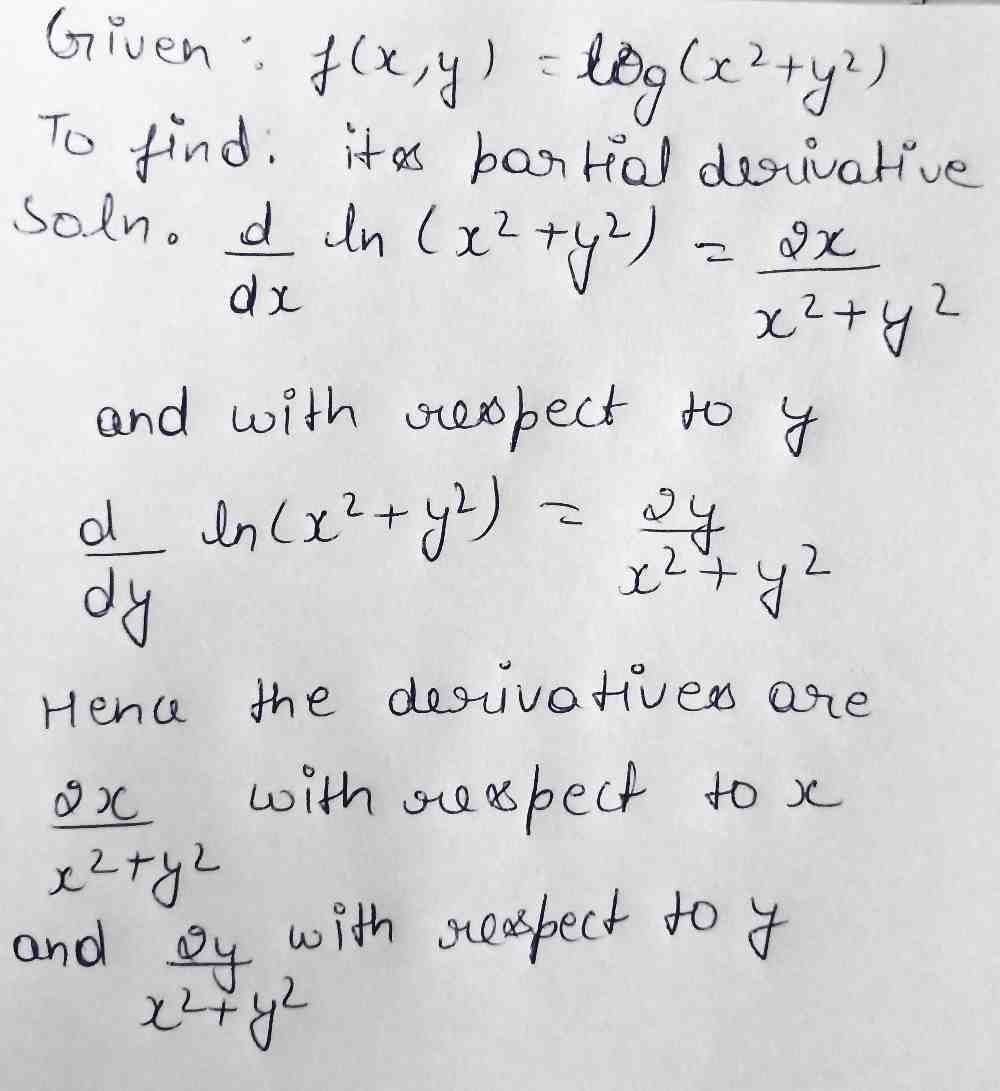



Partial Derivative Of Fx Y Ln X2 Y2 Gauthmath



Http Maths Dur Ac Uk Users Daniel Evans Mes Messolutionsupdated Pdf



Find The Partial Derivatives Of The Following Functions At The Indicated Points I F X Y 3x 2 2xy Y 2 5x 2 2 5 Sarthaks Econnect Largest Online Education Community




Let F R2 R Be Given By Z Y 0 0 R Y 2y And F 0 0 Homeworklib



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero



12 3 Partial Derivatives Mathematics Libretexts




Find The First Order Partial Derivatives Of The Chegg Com



Http Www Utm Utoronto Ca Asc Sites Files Asc Public Shared Pdf Tip Sheets Math Rgasc Cmath Partial derivatives 1117 Pdf



Partial Derivatives




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download




Practice Problems 10 And 11



Partial Derivatives



Http Users Math Msu Edu Users Gnagy Teaching 11 Fall Mth234 L14 234 Pdf



Partial Derivative Wikipedia




Partial Differentiation Application




Second Order Partial Derivatives



Solved Determine The Second Partial Derivatives Of F X Y Z Tan 5 2x2y4z2 Xx 4y42 8x2y422tan 2x2y422 5 1 Sec 2x2y4 2 5 Course Hero




Higher Derivatives Partial Differentiation




Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange
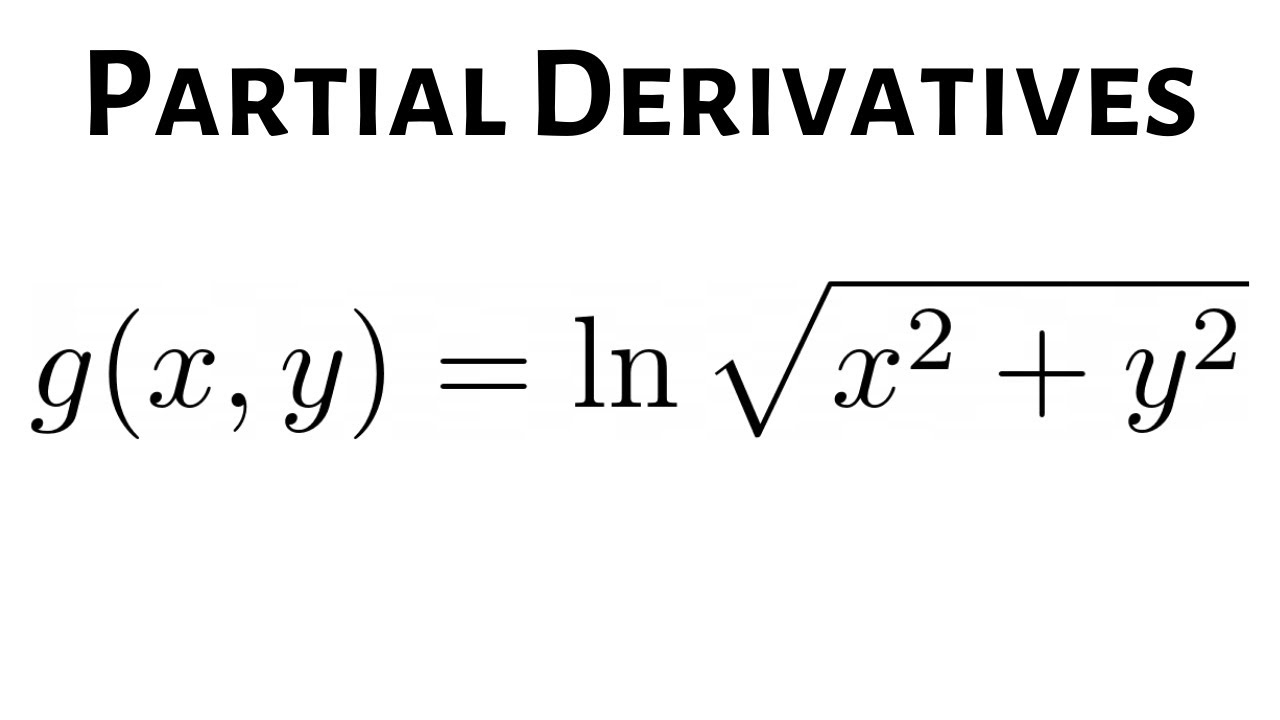



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube




14 Use The Limit Definition Of Partial Derivative To Compute The Partial Deriva Tives Of The Functions At The Specified Points And A F X Y 1 Y 3 C Y At 1 2 B F X Y 4 2x




Partial Derivatives Calculus 3



Www Ualberta Ca Rjia Math214 Part4 Lec2 Pdf



Ocw Mit Edu Ans7870 Textbooks Strang Edited Calculus Study Guide 13 Pdf




Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube




Partial F X Y X F X X2 Y2 And Then We Evaluate The Derivative As If Y Is A Constant Pdf Free Download




Find All The Second Order Partial Derivatives Of The Chegg Com



1



Www Ucl Ac Uk Ucahjva Multi4 Pdf
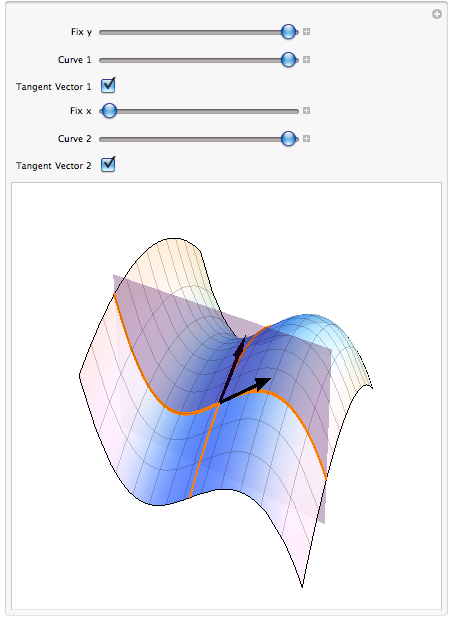



Geometry Of Partial Derivatives



Multivariable Partial Derivative Dp



Find The Indicated Partial Derivative F X Y




Pdf Functions Of Several Variables And Partial Di Erentiation 1 Functions Of Several Variables Mic Mus Academia Edu




Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com
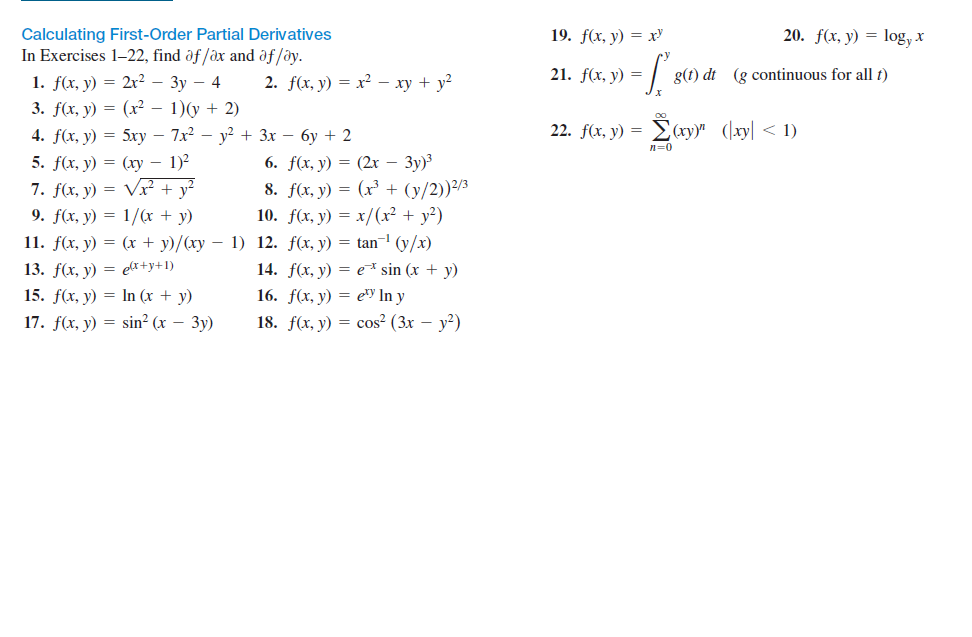



Answered Calculating First Order Partial Bartleby




Derivative Calculator Wolfram Alpha



Partial Derivatives Of Higher Order




Second Order Partial Derivatives




Calc 501 1000 By James Bardo Issuu
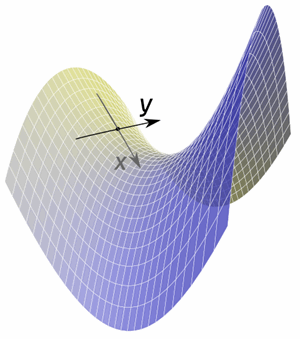



Partial Derivatives
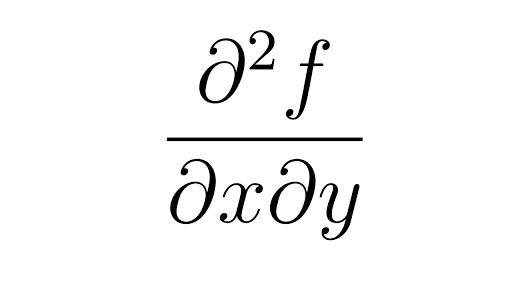



Second Partial Derivatives Article Khan Academy



Rules Of Calculus Multivariate


